Frank-Read Source by Pure Python

We can run the following test case without having to compile OpenDiS.

To run the simulation, simply execute:

cd ${OPENDIS_DIR}
cd examples/02_frank_read_src
python3 -i test_frank_read_src_pydis.py

Initial Condition

The initial configuration of this simulation is a rectangular (prismatic) dislocation loop, where all four sides are of pure edge type. Their Burgers vectors are normal to the plane of the rectangular loop. All four corner nodes have their constraint = pinned (PINNED_NODE). This is sufficient to pin the bottom and two side arms of the prismatic loop. However, the top arm contains a node (in the middle) that is free to move. This allows the top arm to bow out (under the action of applied stress) and act as a Frank-Read source.

The data structure of the initial condition is explained in Section DisNet Class.

Boundary Condition

Periodic boundary condition (PBC) is applied in all three directions, as specified in the following line of the test script.

   net = init_frank_read_src_loop(box_length=Lbox, arm_length=0.125*Lbox, pbc=True)

Simulation Behavior

If the simulation runs successfully, a (Python Matplotlib) window should open and the final dislocation configuration at the end of the simulation should look something like this.

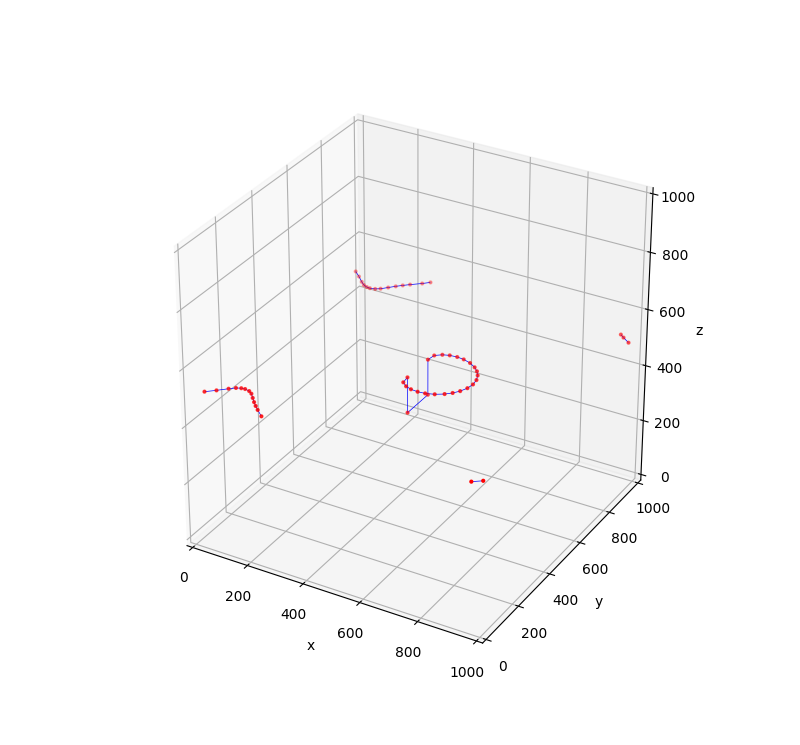
Screenshot of the final configuration

Here is what you should see during the simulation.

Video of the whole simulation

Hint

If you do not see a new window displaying the dislocation configuration, it is possible because you are running on a remote server and didn’t have the X11 forwarding set up correctly. Add the -Y option in your ssh command, such as ssh -Y <your_account>@your.cluster.address. You can also try the xeyes command (which will open a new window) to verify that your X11 channel is set up correctly.

Dislocation Network Examination

Since we ran the test case in Python interactive mode (with the -i option), we can examine the data structure representing the dislocation network (i.e. a graph) at the end of the simulation. For example, use the following command to see all the nodes (DisNode) in the dislocation network (DisNet).

G.all_nodes_tags()

Each node is labeled by a tag, which is a tuple of two integers, (domainID, index). This is following the convention of ParaDiS. In this example, the domainID equals 0 for all nodes. The output of the above command is,

dict_keys([(0, 0), (0, 2), (0, 3), (0, 4), (0, 11), (0, 12), (0, 17), (0, 18), (0, 27), (0, 28), (0, 29), (0, 32), (0, 33), (0, 34), (0, 41), (0, 42), (0, 63), (0, 64), (0, 77), (0, 78), (0, 79), (0, 80), (0, 83), (0, 84), (0, 85), (0, 86), (0, 87), (0, 88), (0, 89), (0, 43), (0, 102), (0, 103), (0, 107), (0, 110), (0, 124), (0, 128), (0, 51), (0, 111), (0, 120), (0, 14), (0, 23), (0, 117), (0, 5), (0, 9), (0, 129), (0, 113), (0, 22), (0, 112), (0, 73), (0, 10), (0, 44), (0, 66), (0, 96), (0, 74), (0, 100)])

Hint

In other test cases, if G is not available, you can use net.G instead, e.g.

net.G.all_nodes_tags()

To examine the information (i.e. attributes) of a node, use the following command, e.g.

G.nodes((0,0)).view()

The output is

{'R': array([500. , 437.5, 500. ]), 'constraint': 7}

Use the following command to see all the segments (DisEdge) in the dislocation network (DisNet).

list(G.all_segments_tags())

The output of the above command is,

[((0, 2), (0, 3)), ((0, 3), (0, 4)), ((0, 4), (0, 0)), ((0, 33), (0, 79)), ((0, 79), (0, 11)), ((0, 12), (0, 80)), ((0, 80), (0, 34)), ((0, 17), (0, 83)), ((0, 83), (0, 33)), ((0, 34), (0, 84)), ((0, 84), (0, 18)), ((0, 41), (0, 87)), ((0, 88), (0, 42)), ((0, 89), (0, 17)), ((0, 103), (0, 2)), ((0, 0), (0, 107)), ((0, 27), (0, 51)), ((0, 51), (0, 77)), ((0, 78), (0, 111)), ((0, 111), (0, 28)), ((0, 11), (0, 120)), ((0, 120), (0, 63)), ((0, 64), (0, 14)), ((0, 14), (0, 12)), ((0, 102), (0, 23)), ((0, 23), (0, 86)), ((0, 77), (0, 117)), ((0, 117), (0, 41)), ((0, 42), (0, 5)), ((0, 5), (0, 78)), ((0, 43), (0, 9)), ((0, 9), (0, 110)), ((0, 32), (0, 129)), ((0, 129), (0, 124)), ((0, 124), (0, 22)), ((0, 22), (0, 43)), ((0, 110), (0, 112)), ((0, 112), (0, 85)), ((0, 73), (0, 27)), ((0, 28), (0, 10)), ((0, 86), (0, 44)), ((0, 44), (0, 103)), ((0, 32), (0, 66)), ((0, 66), (0, 128)), ((0, 107), (0, 96)), ((0, 96), (0, 85)), ((0, 128), (0, 74)), ((0, 74), (0, 102)), ((0, 29), (0, 63)), ((0, 100), (0, 87)), ((0, 64), (0, 113)), ((0, 10), (0, 113)), ((0, 18), (0, 89)), ((0, 29), (0, 73)), ((0, 100), (0, 88))]

We can see that each segment is specified by the tags of its two end nodes. Each segment is included only once in this representation.

To examine the information (i.e. attributes) of a segment, use the following command, e.g.

G.segments(((0,0),(0,4))).view()

The output is

{'source_tag': (0, 4), 'burg_vec': array([1., 0., 0.]), 'plane_normal': array([ 0., -1.,  0.])}

Note that each segment needs to know the line direction corresponding to the Burgers vector being stored. The line direction goes from the node designated by source_tag.

We can use the burg_vec_from function to obtain the Burgers vector using either one of the two end nodes, e.g.

G.segments(((0,0),(0,4))).burg_vec_from((0,4))

The output is

array([1., 0., 0.])

Alternatively,

G.segments(((0,0),(0,4))).burg_vec_from((0,0))

The output is

array([-1., -0., -0.])

We can also examine the information for the simulation cell as follows.

G.cell.view()

The output of the above command is,

{'h': array([[1000.,    0.,    0.],
       [   0., 1000.,    0.],
       [   0.,    0., 1000.]]), 'hinv': array([[0.001, 0.   , 0.   ],
       [0.   , 0.001, 0.   ],
       [0.   , 0.   , 0.001]]), 'origin': array([0., 0., 0.]), 'is_periodic': [True, True, True]}